In the previous post I ran through why it makes sense to run onboarding experiments and measuring them under an A/B or A/A/B methodology. I stuck to the qualitative principles and didn’t get “into the weeds” of the math. However, I promised to follow up with an explanation of statistical significance for the geek minded.
Because A/B has been around for a very long time in various “web” fields such as landing page optimisation, email blasts and advertising – this is by far the first, last or most useful. The purpose here is to:
- tightly couple the running onboarding and educations to a purpose, and that is:
- Make onboarding less “spray and pray” and head towards more ordered directions of continuous improvement
- deepen user engagement with your App’s features.
- Explain the reason why the Contextual Dashboard presents these few metrics rather a zillion pretty charts that don’t do anything other than befuddle your boss.
In this case, we will consider a simple A/B test (or Champion vs Challenger).
Confidence for statistical significance
Back to that statistics lecture again (my 2nd-year engineering statistics class was in evenings and usually preceded by a student’s meal of boiled rice, soy sauce and Guinness (the nutrition element) – so I’ll rely more on Wikipedia than my lecture notes 🙂
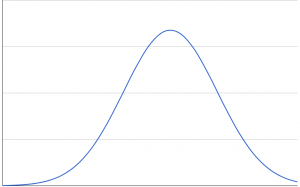
If you think about your A and B experiments, you should get a normal distribution of behaviour – plotting on the chart you get the mean which is the center point of the curve and a population that is plotted either side of the center – yielding a chart like this.
Confidence Interval is the range of values in a normal distribution than that fit a percentage of the population. In the chart below, 95% of the population is in blue.
Most commonly the confidence interval of 95% is used, here is what Wikipedia says about 95% and 1.96:
95% of the area under a normal curve lies within roughly 1.96 standard deviations of the mean, and due to the central limit theorem, this number is therefore used in the construction of approximate 95% confidence intervals.
The Math by Example
Let’s take a simple example of an App that is in its default state as the engineers have delivered it, there is a new feature that has been delivered but the Product Manager wants to increase the uptake and engagement of the feature. The goal is to split the audience and measure the uplift of the feature.
We call the usage of the new feature a “convert” and a 10% conversion rate means that 10% of the total population in the “split matches”.
CHAMPION
This is the App’s default state.
- T = 1000 split matches
- C = 100 convert (10% conversion rate).
- 95% range ⇒ 1.96
The standard error for the champion:
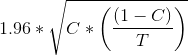
Standard Error (SE) = 1.96 * 0.00949 = 0.0186
- C ± SE
- 10% ± 1.9% = 8.1% to 11.9%
CHALLENGER:
This is the App’s default state PLUS the Product Manager’s tip/tour/modal to educate users about this awesome new feature.
- T = 1000 split matches
- C = 150 convert (15% conversion rate)
- 95% range ⇒ 1.96
SE (challenger)
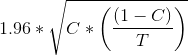
Standard Error (SE) =1.96 * 0.01129 *= 0.02213
- C ± SE
- 15% ± 2.2% = 12.8% to 17.2%
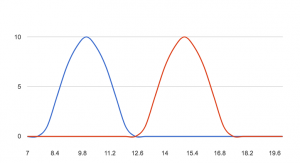
Now charting these 2 normal distributions to see the results. Thus, since there is no overlap using the 95%/1.96 confidence, the variation results are accepted as reliable. (I couldn’t figure out how to do the shading for the 95%!)
In this case you can conclude that the A/B test has succeeded with a clear winner and can be declared as a new champion. If you refer back to the last post, then iteration can be part of your methodology to continuously improve.
How long should an experiment run?
Experiments should run to a statistical conclusion, rather than rubbing your chin and saying “lets run it for 3 days” or “lets run it in June” – period based decisions are logical to humans but that has nothing to do with the experiment**.
So my example above is technically not helpful if the data hadn’t provided a conclusive result – this is argued in a most excellent paper from 2010 by Evan Miller. Vendors of dashboard products like ours can encourage the wrong behaviour by tying the experiment to a time period
** except for the behaviour of your human subjects – like your demographic are all on summer holidays